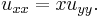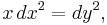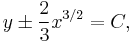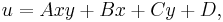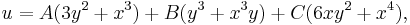Euler–Tricomi equation

In mathematics, the Euler–Tricomi equation is a linear partial differential equation useful in the study of transonic flow. It is named for Leonhard Euler and Francesco Giacomo Tricomi.

$u_{xx}=xu_{yy}. \,$

It is hyperbolic in the half plane x > 0, parabolic at x = 0 and elliptic in the half plane x < 0. Its characteristics are

$x\,dx^2=dy^2, \,$

which have the integral

$y\pm\frac{2}{3}x^{3/2}=C,$

where C is a constant of integration. The characteristics thus comprise two families of semicubical parabolas, with cusps on the line x = 0, the curves lying on the right hand side of the y-axis.

Particular solutions

Particular solutions to the Euler–Tricomi equations include

$u=Axy %2B Bx %2B Cy %2B D, \,$
$u=A(3y^2%2Bx^3)%2BB(y^3%2Bx^3y)%2BC(6xy^2%2Bx^4), \,$

where A, B, C, D are arbitrary constants.

The Euler–Tricomi equation is a limiting form of Chaplygin's equation.

External links

Tricomi and Generalized Tricomi Equations at EqWorld: The World of Mathematical Equations.

Bibliography

A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, 2002.